Resistance is Everything

🔖 Background Information

A resistor is a piece of electronics equipment that resists the flow of electricity in a circuit. Different resistors can resist electrical flow with different strengths. This strength of resistance is measured in units of ohms (\(\Omega\)).

Generally, a circuit will not have just one resistor. Rather, it will have two or more resistors in different configurations. The total resistance (a.k.a the equivalent resistance) of the circuit depends on how the resistors are connected together.

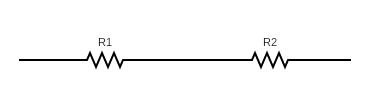
Resistors In Series

Two resistors can be placed in line with one another. This is called placing them “in series”.

Two resistors in series will will have an equivalent resistance given by:

\[R_{eq} = R_1 + R_2\]

This is read: “the equivalent resistance of two resistors placed in series is equal to the sum of the resistance strengths of the two resistors.

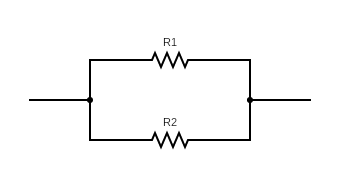
Resistors Placed In Parallel

On the other hand, two resistors can also be placed side by side. This is called placing them “in parallel”.

In this configuration, the equivalent resistance is given by:

\[R_{eq} = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2}}\]

This is read: “the equivalent resistance of two resistors placed in parallel is the reciprocal of the sum of the reciprocals of the individual resistances”.

🎯 Problem Statement

Given a user’s input of two resistances, calculate the equivalent resistance of the two resistors in series and parallel.

✅ Acceptance Criteria

• When I execute the program, I should see a welcome prompt.
• Then, the program should ask me to enter two values for resistances. The way that you take this input is up to you - they can be separated by a space or the user might be prompted multiple times for inputs.
• After I give my input, the program should repeat the two values that I provided in a sentence.
• Then, the program should print out the equivalent resistance of the two resistors in series and in parallel.
• Finally, I should see an exit message as the program gracefully exits.

📋 Dev Notes

There are no dev notes for this problem.

🖥️ Example Output

$ ./resist.out

Welcome to the Resistor Calculation Program!

Please enter your two resistances:  12 42
Thank you! You have entered 12 ohms and 42 ohms!

If your resistors are placed in series, they will total to 54 ohms.
If they are placed in parallel, they will total 9.333333 ohms.

Thank you for using the RCP!

📝 Thought Provoking Questions

1. How many cin statements did you end up using in this program? Could you have gotten away with fewer cin statements? What are the tradeoffs of using more or fewer cin statements?
2. Does it matter what order the user types their two resistance values into your program? For example, would I get the same answer if I first typed in \(10 \: \Omega\) and then \(20 \: \Omega\) versus \(20 \: \Omega\) then \(10 \: \Omega\)? Why or why not?
3. Should the “welcome” message and the “enter” prompt be printed from the same cout statement? Why or why not?
4. In the mathematical notation of the equivalent parallel resistance formula, the division bar acts as a grouping symbol. How do you ensure that the sum in the denominator of this complex rational expression is treated as a single group when translating the formula into a C++ expression?
5. Recall that domain restrictions can come from both the algebraic operations in an expression as well as real-world concerns. What values are not allowed mathematically for \(R_1\) and \(R_2\)?
6. What would happen if the user typed in a negative value for a resistance? Note, you do not need to write any code to handle this case.
7. What would happen if the user typed in zero for a resistance? Note, you do not need to write any code to handle this case.

💼 Add-Ons For the Portfolio

(One Credit) Algebraic Exploration

The formulae that were given above for the equivalent resistance calculations are what you would see in most introductory electronic circuits textbooks. However, they are not necessarily optimal for implementation on a computer. Specifically, the equation for the series configuration is fine, but the one for the parallel configuration is not optimal. The equation for the parallel configuration requires three divisions, and division can be slow on a computer.

Rearrange the equation for the parallel configuration to require only one division and one multiplication instead of three divisions. Then, refactor your program to use the new formula. The program should run in the same way as before, besides the small optimization.

Hint: Start with the equation \(\frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2}\) and solve for \(R_{eq}\). Simplify the right side of the equation and then take the inverse of both sides.

(One Credit) Multiple Prompts

It can be cumbersome for a user to enter two values in one prompt. Refactor your program to use two prompts instead of one:

1. Ask users for the values of \(R_1\) and \(R_2\) with two separate cin statements.
2. For each prompt, a user will enter a bare number, just like before.
3. The rest of the program should run in the same way as before.

$ ./resist.out

Welcome to the Resistor Calculation Program!

Please enter your first resistance: 12
Please enter your second resistance: 42
Thank you! You have entered 12 ohms and 42 ohms!

If your resistors are placed in series, they will total to 54 ohms.
If they are placed in parallel, they will total 9.333333 ohms.

Thank you for using the RCP!

(Two Credits) User Entered Units

Sometimes, people like to enter units of “ohms” as part of their input. Refactor the program to do the following:

1. Ask users for the values of \(R_1\) and \(R_2\) with two separate cin statements.
2. For each prompt, a user can either enter a bare number (e.g. 12) or a number with units (e.g. 12 ohms).
3. The rest of the program should run in the same way as before.

$ ./resist.out

Welcome to the Resistor Calculation Program!

Please enter your first resistance: 12 ohms
Please enter your second resistance: 42
Thank you! You have entered 12 ohms and 42 ohms!

If your resistors are placed in series, they will total to 54 ohms.
If they are placed in parallel, they will total 9.333333 ohms.

Thank you for using the Resistor Calculation Program!

Note: If you complete this challenge, you will automatically earn credit for “Multiple Prompts” as well!

🔗 Useful Links

• C++ Project Template

📘 Works Cited

This problem is available courtey of Professor Jason James (James).

1. James, Jason. “Resistance Is Everything.” Jason James’ Homepage, http://craie-programming.org/121/labs/resist.simp.html, February 2023.